Questões de Fundamentos de Óptica

Sombra e Penumbra

1. Uma pessoa de 1,9 m de altura está em pé ao lado de um prédio. A sombra do prédio projetada pela luz solar é de 90 m enquanto a da pessoa é de 9 m. Qual a altura do prédio?

Começamos o problema pensando nos raios solares, uma vez que devem incidir paralelamente entre si. A pessoa, a sombra e o raio de luz formam um triângulo retângulo assim como o triângulo formado pelo prédio, sombra e raio de luz; os ângulos formados devem ser os mesmos. Assim podemos escrever uma semelhança de triângulos:

Podemos isolar a altura do prédio e calculá-la em função dos dados conhecidos:

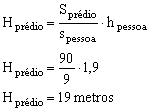
2. Uma lâmpada é usada para iluminar uma sala de 3 m de altura entre o chão e o teto. A uma altura de 1 m do chão está uma mesa quadrada com cada lado medindo 40 cm. Supondo que a lâmpada seja uma fonte puntual localizada exatamente ao centro da mesa, qual a área da sombra da mesa?

Nesta situação podemos analisar a distância entre o centro da mesa e uma das extremidades. Ficamos com a diferença entre a mesa e o teto igual a 2 m e a largura média da mesa igual a 20 cm. Assim, encontraremos o valor de x e com isto as dimensões da sombra.

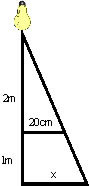
Usando semelhança de triângulos:

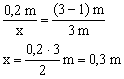
Sabemos que esta é a metade da dimensão da sombra, logo, a dimensão total projetada é de 0,6 m, de onde podemos calcular a área da sombra:

Câmara escura de orifício

1. Um objeto de 20 cm de tamanho é colocado a uma distância de 4 m de uma câmara com uma orifício cuja dimensão entre a entrada e o anteparo é de 50 cm. Qual o tamanho do objeto projetado no anteparo? Ele estará invertido?

Primeiramente devemos interpretar os dados do problema. A distância entre o objeto e a entrada da câmara é p, a distância entre a entrada e o anteparo é p' e o tamanho do objeto é o. Assim, basta aplicar a fórmula da câmara escura:

Isolando o tamanho da imagem, i:

Basta aplicar os valores, lembrando de utilizar a mesma unidade para todas as grandezas!