Modelo quântico para as radiações eletromagnéticas
A teoria eletromagnética de Maxwell é muito útil para explicar os fenômenos relacionados à propagação das radiações eletromagnéticas. Entretanto, não serve para explicar alguns fenômenos que ocorrem na interação dessas radiações com a matéria, tampouco alguns fatos relacionados à emissão.
Um exemplo disso é o espectro de emissão do corpo, que foi objeto de estudo de muitos cientistas durante meio século, uma vez que as ideias da época apresentavam incoerências entre as previsões teóricas e os resultados experimentais.
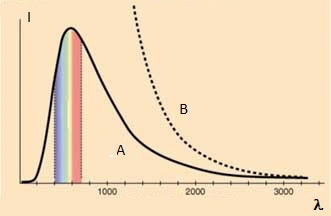
Legenda:
- A: curva obtida a partir de resultados experimentais;
- B: curva prevista pela teoria clássica.
O fato do comportamento do gráfico da intensidade da radiação do corpo negro em função do comprimento de onda previsto por Maxwell ser muito diferente do obtido por meio de dados experimentais ficou conhecido, no século XIX, como catástrofre do violeta.
Em 1900, Max Planck apresentou uma nova teoria, que entrava em conflito com a teoria clássica aceita até então, com o objetivo de solucionar o problema. Planck supôs que, na superfície de um corpo negro, havia osciladores harmônicos simples (OHS, representados pelas cargas elétricas oscilantes) capazes de assumir determinados valores de energia. Matematicamente:
![]()
Onde:
n = número quântico;
h = constante de Planck (h = 6,63x10-34 J.s);
f = frequência do oscilador.
Cada valor de n representará um estado quântico diferente desse oscilador e será sempre um múltiplo de hf, o que significa que a energia do oscilador é quantizada, isto é, só pode assumir certos valores.
De acordo com a Física Clássica, um OHS pode ter qualquer valor de energia e não depende da frequência, e sim da amplitude das oscilações. Isso torna a atitude de Planck de propor uma nova teoria contrária a esses princípios bastante corajosa. Além disso, ele propôs que os OHS existentes na superfície do corpo emitem ou absorvem energia apenas ao passarem de um estado quântico para outro.
Assim, se o oscilador passa de um nível maior de energia para um nível menor, por exemplo, de n=2 para n=1, ele emite uma quantidade discreta de energia, que corresponde, matematicamente, à diferença entre as energias dos dois níveis. Caso passe de um nível de menor de energia para um de maior, como de n=1 para n=2, ele absrove uma quantidade discreta de energia, analogamente ao caso anterior. Isso significa que a emissão e absorção de energia também ocorrem em quantidades quantizadas.
Cada porção discreta de energia foi denominada quantum, termo que vem do latim, cujo plural é quanta. Em virtude isso, a teoria de Planck ganhou popularidade com o nome de teoria dos quanta.
Utilizando-se as formulações feitas por Max Planck para a quantização de energia, foi possível obter-se um novo gráfico de intensidade da radiação emitida pelo corpo em função do comprimento de onda em pleno acordo com os resultados experimentais.
Entretanto, uma nova questão perturbava os físicos da época: se a energia é emitida apenas em quantidades bem determinadas, o que implica determinados comprimentos de onda e frequências bem estabelecidos, como o espectro da radiação térmica pode ser contínuo? A resposta é a seguinte: como há um número muito grande de osciladores com energias distintas, a probabilidade de serem emitidas radiações de quaisquer frequências também é muito grande.
Vale salientar que Planck nunca afirmou que as radiações eletromagnéticas se propagavam em quantidades discretas de energia. Nesse ponto de vista, ele acreditava que a teoria proposta por Maxwell era coerente. Portanto, para Planck, quantizados eram os osciladores, e não a radiação eletromagnética.
É importante que saibamos que a ideia do quantum, mais tarde denominado fóton, foi muito útil para esclarecer diversos outros fenômenos que a Física Clássica não era capaz de explicar corretamente.





























